Particle gradient flows

Many tasks in machine learning and signal processing require to minimize a convex function of a measure:

\[ \min_{\mu \in \mathcal{M}(\Theta)} J(\mu) \]

where \(\mathcal{M}(\Theta)\) is the space of measures on a manifold \(\Theta\). We focus on the case where \(J\) is (weakly) continuous and (Fréchet) differentiable. For this optimization problem, we investigate the method that consists in discretizing the measure into particles \(\mu = \sum_{i=1}^m w_i \delta_{\theta_i}\) and taking the gradient flow of \(J\) in the parameters \((w_i,\theta_i)_i\). We show that, quite generically, this gradient flow converges to global minimizers in the many-particle limit \(m \to \infty\), if the initial distribution of particles is satisfies a “separation” property.

Animations

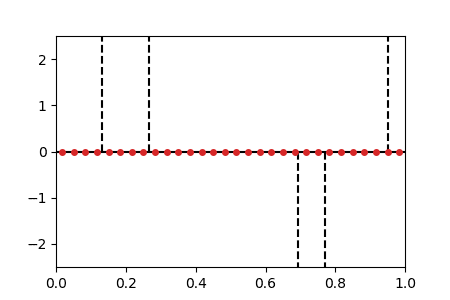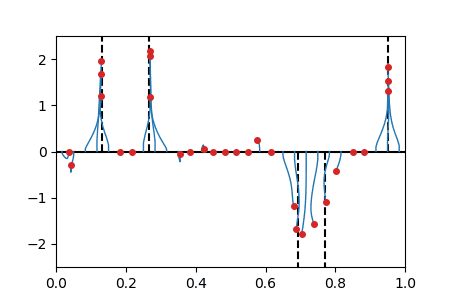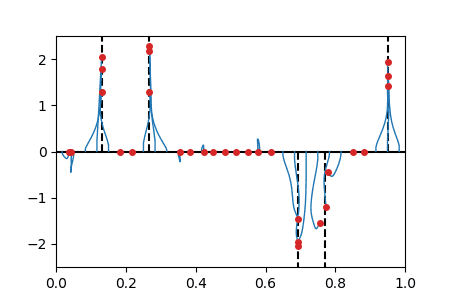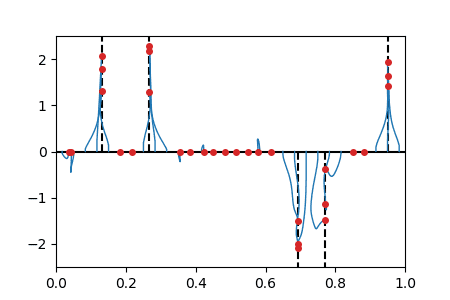
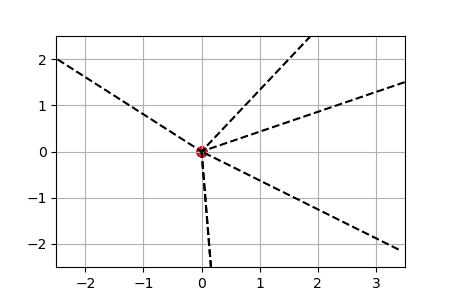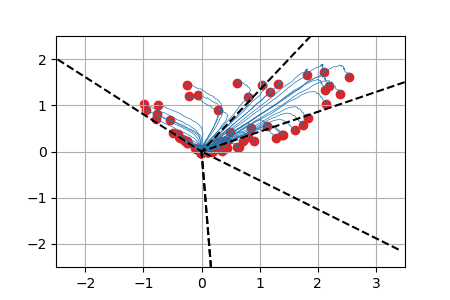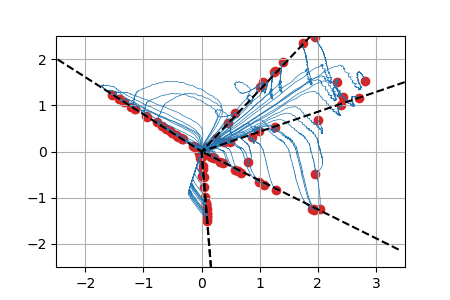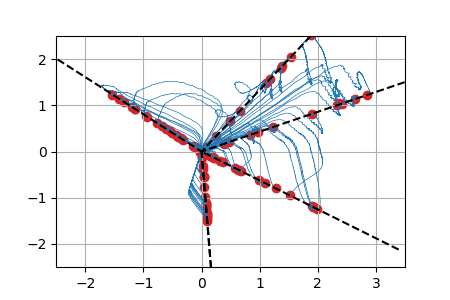
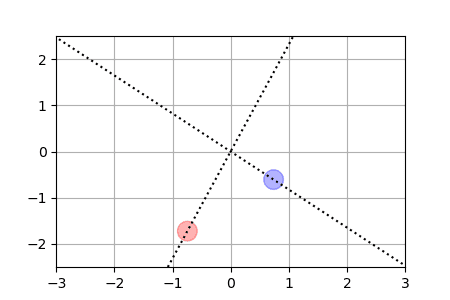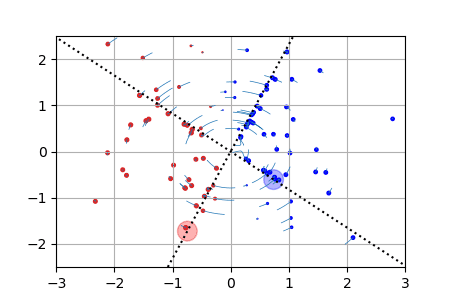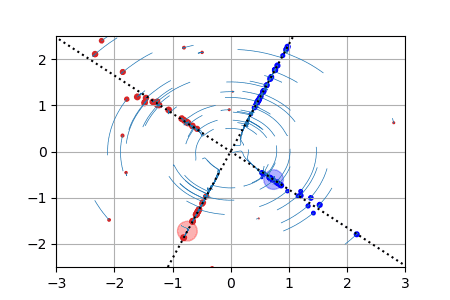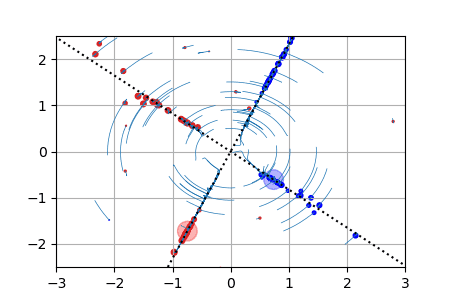
We display below animated versions of the particle gradient flows shown in Section 4 of the preprint, as well as a particle gradient flow corresponding to the training of a neural network with a single hidden layer and sigmoid activation function in dimension d=2. In all these cases, the global minimizer (supported on the dotted lines in the plots) is found. The time scale is logarithmic (see paper for details).

Sparse spikes deconvolution

We solve the BLASSO problem for recovering a sum-of-impulse signal given noisy and filtered observations. The method corresponds to a non-convex forward-backward method on the vector of position/weights of all particles. The positions \(\theta(t)\) of the particles are shown horizontally and weight \(w(t)\) shown vertically. The initialization is evenly spaced on \(\{0\} \times [0,1]\) (this satisfies asymptotically the separation condition).

Neural networks with a single hidden layer

We train a simple neural network on a synthetic well-specified model with SGD.

ReLU activation function: we show for each particle the trajectory \(\vert w(t)\vert\cdot \theta(t)\in \mathbb{R}^2\). The initialization is uniformly random on a sphere around \(0\) (this satisfies asymptotically the separation condition). This case has a homogeneous structure and is treated separately in the paper.

Sigmoid activation function: weights \(w(t)\) represented by the size of the particles (blue for negative, red for positive, ground truth shown with 2 neurons shown by large disks). The initialization is distributed according to a normal law on \(\mathbb{R}^2\) (this satisfies asymptotically the separation condition).